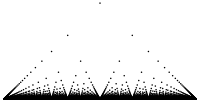
Функция Римана на промежутке от 0 до 1
Эта функция имеет и много других названий: функция Томе (примеч. Carl Johannes Thomae (1840 – 1921) — немецкий математик), модифицированная функция Дирихле, поп-корн (popcorn) функция, функция дождевых капель (raindrop), функция счетных облаков (countable cloud), функция линейки (ruler) или Звезды над Вавилоном (Stars over Babylon).
Функция Римана является простейшим примером функции, которая непрерывна во всех иррациональных точках и разрывна во всех рациональных точках. Эта вещественнозначная функция одной переменной определяется так:
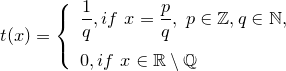
(здесь дробь  несократима). несократима).
Докажем, что функция Римана непрерывна во всех иррациональных точках. Действительно, для данного иррационального числа  и произвольного и произвольного 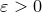 рассмотрим множество рассмотрим множество
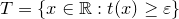 . .
Если 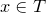 , то , то 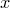 — рациональное число вида — рациональное число вида 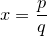 , где , где 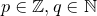 , дробь , дробь 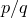 несократима и несократима и 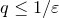 . Из ограничения на . Из ограничения на 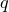 следует, что пересечение множества следует, что пересечение множества 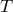 и промежутка и промежутка 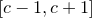 состоит из конечного числа точек. Таким образом, мы можем выбрать окрестность точки состоит из конечного числа точек. Таким образом, мы можем выбрать окрестность точки  так, чтобы в ней не содержалась ни одна точка множества так, чтобы в ней не содержалась ни одна точка множества 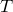 . А если . А если 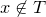 , то , то 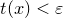 . Отсюда следует доказываемое. . Отсюда следует доказываемое.
Теперь докажем, что функция Римана разрывна во всех рациональных точках. Действительно, существует хотя бы одно иррациональное число сколь угодно близко к любому рациональному числу. Тем самым, мы можем выбрать последовательность иррациональных чисел, стремящуюся к данному рациональному числу. Тогда предел соответствующих значения функции (для членов данной последовательности) будет равен нулю, что отличается от значения функции и данной точке.
Интересно, что функции, непрерывной во всех рациональных точках и разрывной во всех иррациональных точках, не существует.
Читать полностью:http://www.km.ru/referats/333589-funktsiya-rimana |